병합 정렬이란?
"병합 정렬(Merge Sort)"은 "분할 정복" 전략을 기반으로 하는 효율적인 정렬 알고리즘입니다. 이 알고리즘은 입력 배열을 더 작은 하위 배열로 재귀적으로 나눈 후, 각 하위 배열을 정렬하고, 다시 병합하면서 전체 배열을 정렬하는 방식으로 동작합니다. 특히 "병합 정렬"은 안정 정렬(stable sort)에 해당하며, 입력 배열의 원소 순서가 동일한 값일 경우에도 유지된다는 특성을 가집니다. 또한 최악의 경우에도 시간 복잡도가 일정하여 매우 안정적인 성능을 보입니다.
"안정 정렬"이란, 값이 같은 항목이 있을 때 원래의 입력 순서를 그대로 유지하는 정렬을 말합니다. 예를 들어 이름과 점수를 함께 정렬하는 상황에서, 점수가 같은 학생들의 이름 순서를 유지할 수 있는 정렬 방식이 안정 정렬입니다.
핵심 원리
"분할 정복" 구조
"병합 정렬"은 세 단계로 이루어진 "분할 정복(Divide and Conquer)" 구조를 따릅니다.
- Divide (분할): 배열을 정확히 반으로 나누어 더 작은 부분 문제로 쪼갭니다. 이 작업은 배열의 길이가 1이 될 때까지 반복됩니다.
- Conquer (정복): 분할된 배열이 더 이상 나눌 수 없는 수준(길이 1 이하)에 도달하면, 해당 배열은 정렬된 것으로 간주합니다.
- Combine (병합): 각 정렬된 하위 배열을 병합하며 하나의 정렬된 배열로 합칩니다. 이 과정에서 크기 비교를 통해 정렬된 형태를 유지합니다.
이러한 방식은 재귀 호출을 통해 매우 자연스럽게 구현됩니다.
JavaScript로 구현하기
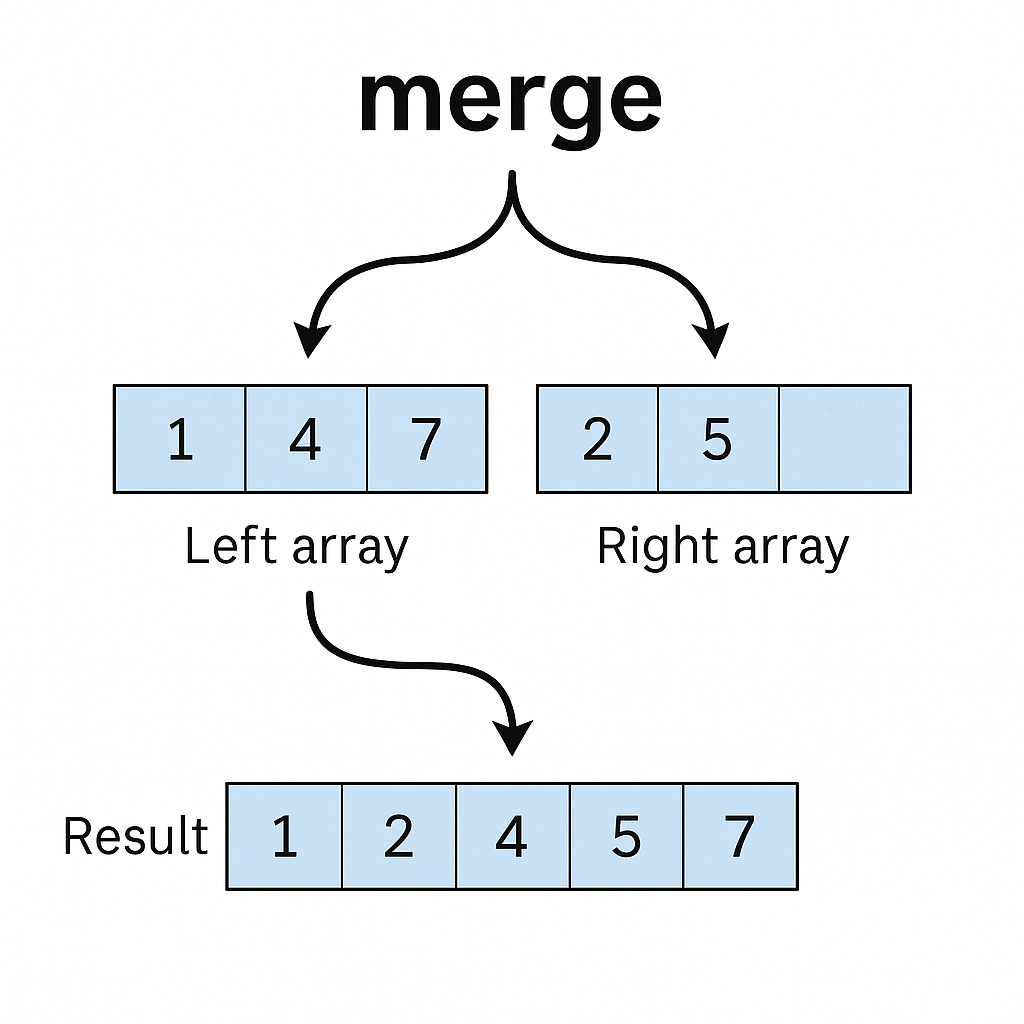
merge 함수
// 두 개의 정렬된 배열을 병합하는 함수
function merge(left, right) {
const result = []; // 결과 배열 초기화
let i = 0, j = 0; // left와 right 배열의 인덱스 포인터
// 양쪽 배열의 요소를 비교하며 작은 값을 결과에 추가
while (i < left.length && j < right.length) {
if (left[i] < right[j]) {
result.push(left[i]);
i++;
} else {
result.push(right[j]);
j++;
}
}
// 남은 요소들을 결과 배열에 추가
return result.concat(left.slice(i)).concat(right.slice(j));
}
mergeSort 함수
// 병합 정렬의 재귀 함수
function mergeSort(arr) {
if (arr.length <= 1) return arr; // 더 이상 분할 불가한 경우 base case
const mid = Math.floor(arr.length / 2); // 배열을 반으로 나눌 중간 인덱스
const left = arr.slice(0, mid); // 왼쪽 하위 배열
const right = arr.slice(mid); // 오른쪽 하위 배열
// 각 하위 배열을 재귀적으로 정렬한 뒤 병합
return merge(mergeSort(left), mergeSort(right));
}
// 예제 실행
const sample = [38, 27, 43, 3, 9, 82, 10];
console.log("정렬 결과:", mergeSort(sample));출력 결과
정렬 결과: [3, 9, 10, 27, 38, 43, 82]시각 자료로 보는 정렬 과정
병합 정렬은 다음과 같은 흐름을 따릅니다.
[38, 27, 43, 3, 9, 82, 10]→ 분할 →[38, 27, 43]+[3, 9, 82, 10][38, 27, 43]→[38]+[27, 43]→[27]+[43][3, 9, 82, 10]→[3, 9]+[82, 10]→[3]+[9],[82]+[10]- 이후 병합하면서 정렬:
[27, 38, 43],[3, 9, 10, 82]→[3, 9, 10, 27, 38, 43, 82]
이처럼 "분할 정복", "재귀 호출", "정렬된 결과 배열"을 단계적으로 구현하는 과정이 명확히 드러납니다.
시간 및 공간 복잡도
- 시간 복잡도: O(n log n)
- 입력 배열을 반으로 나누는 분할 단계가 log n 번 반복되고, 각 병합 단계에서 n 개의 요소를 비교하므로 전체 시간 복잡도는 O(n log n)입니다.
- 공간 복잡도: O(n)
- 정렬된 결과를 저장하기 위한 보조 배열이 필요하기 때문에 추가적인 메모리 공간이 요구됩니다.
병합 정렬은 "in-place 정렬"이 아니기 때문에, 메모리 측면에서는 퀵 정렬보다 효율이 떨어질 수 있습니다.
퀵 정렬과의 차이
| 비교 항목 | 병합 정렬 | 퀵 정렬 |
|---|---|---|
| 평균 시간 복잡도 | O(n log n) | O(n log n) |
| 최악의 경우 | O(n log n) | O(n^2) |
| 안정 정렬 여부 | 예 | 아니오 |
| 공간 효율성 | 낮음 (O(n) 필요) | 높음 (in-place 정렬) |
"병합 정렬"은 항상 일정한 시간 복잡도를 보장하기 때문에 예측 가능한 성능이 중요한 상황에 적합합니다. 반면, "퀵 정렬"은 평균적으로 빠르지만, 특정 케이스에서는 매우 비효율적일 수 있습니다.
실제 활용 사례
- 링크드 리스트 기반 정렬: 임의의 위치에 접근이 어려운 링크드 리스트에서 효율적인 정렬을 제공함.
- 외부 정렬: 전체 데이터를 메모리에 올릴 수 없는 경우 디스크 기반 정렬에 활용됨.
- 금융, 의료 데이터 처리: 데이터의 정렬 순서 보존이 중요한 시스템에서 활용.
마무리 및 CTA
"병합 정렬"은 정렬 알고리즘 중에서도 특히 안정성과 이론적 완성도가 뛰어난 방법입니다. 재귀적 구조 덕분에 코드가 간결하고, 예측 가능한 시간 복잡도로 대규모 데이터 처리에 적합합니다. 정렬 문제를 보다 깊이 이해하려면 병합 정렬을 시작으로 "퀵 정렬", "힙 정렬" 등 다른 정렬 알고리즘과의 비교 학습이 효과적입니다.
추천 학습 자료:
정렬 알고리즘의 구조와 작동 원리를 체계적으로 학습하고 싶다면, 위 자료를 통해 시각화와 함께 연습하는 것을 권장합니다.
'Programing > Algorithm' 카테고리의 다른 글
| JavaScript로 배우는 유클리드 호제법 (GCD with Euclidean Algorithm) (1) | 2025.06.09 |
|---|---|
| JavaScript로 이해하는 프림 알고리즘 (Prim’s Minimum Spanning Tree) (1) | 2025.06.05 |
| JavaScript로 이해하는 크루스칼 알고리즘 (Minimum Spanning Tree) (0) | 2025.06.05 |
| JavaScript로 이해하는 회의실 배정 문제 (Meeting Room Scheduling) (0) | 2025.06.04 |
| JavaScript로 해결하는 활동 선택 문제 (Activity Selection Algorithm) (0) | 2025.06.03 |
| JavaScript로 해결하는 거스름돈 문제 (Greedy Algorithm) (1) | 2025.06.03 |
| JavaScript로 해결하는 0/1 배낭 문제 (Knapsack Problem) (1) | 2025.06.03 |
| JavaScript로 해결하는 동전 교환 문제 (Coin Change Algorithm) (2) | 2025.06.03 |